Teaching the Concept of Time - Effectively!

 

What is time all about?

 

In my own teaching experience across a range of primary year levels and when lecturing pre-service teachers, one of the most frequent displays of a lack of connection between mathematical concepts and poor pedagogical experiences is within the topic of time. Particularly in the year levels between two and four, many primary school students cannot identify the relationships between underlying concepts such as fractions, multiplicative thinking, and the symbolic relationships of number; yet are expected to calculate, read and problem solve with time efficiently from early on in their primary years.

 

In comparison to many other mathematical concepts children explore between years’ two to four, explicit research of how students learn to construct the multiple concepts of time; even the acknowledgement of how complex this learning is, seems vastly underrepresented. However, throughout the available literature there are some key themes teachers need to take into consideration to teach the concept of time effectively.

 

A poor understanding of time can be attributed to poor pedagogical choices; that is, learning experiences that take a superficial perspective such as focusing on "reading" the position of clock hands correctly rather than explicitily learning the range of underlying concepts to construct knowledge on how and why time is measured and represented. Booker, Bond, Sparrow and Swan (2010) explains that the broader topic of time encompasses 3 key areas for conceptual development:

 

1. the concept of duration and passing of time

2. knowledge of sequence and order in time

3. clock face reading 

 

According to Friederwitzer & Berman (1999), the introduction of formal time measuring instruments prematurely (such as a two-hand analogue clock) can result in students learning misconceptions on the purpose and necessity for measuring and solving problems of time. This point is relevant within the current context of the Australian Curriculum as students within the early years of schooling do typically get introduced and expected to work with analogue clocks very quickly - as reflected in the F-2 Australian Curriculum standards. Often is the case that traditional analogue clocks are introduced before students have had a chance to formally construct stable counting principles and number relationships, let alone consider what the notion of time is and how and why we measure it.

 

Friederwitzer et.al (1999) describe the importance of students in early primary schooling exploring concrete time teaching models that make explicit connections with fractions – specifically, concrete models for part-whole relationships of time, measuring and representing units of time and to represent duration and the passing of time. This illustrates the disconnection between concepts many students experience, in that generally, learners who cannot explain, expand on or problem solve with time cannot do so because they have not yet made sense of it concretely.

 

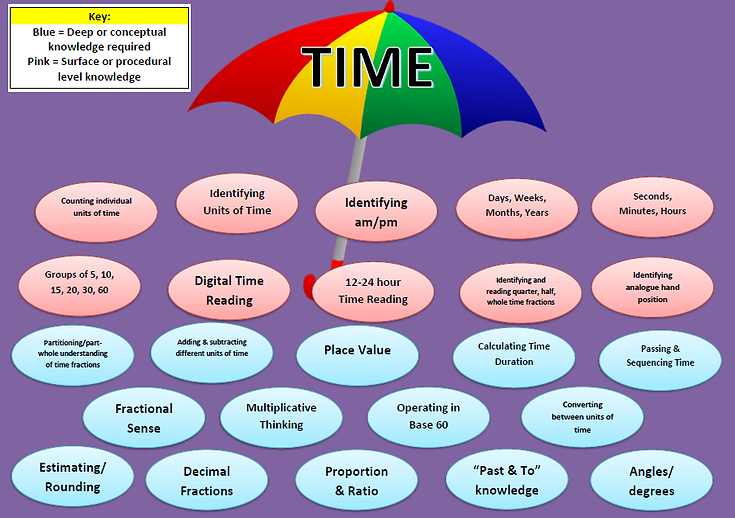
It is claimed that concrete models allow students to construct schema and mental referents for their future ability to work abstractly with time, because they are ‘proving’ and representing time concepts concretely. According to Mathews (2010), due to the complexity of time perception as a cognitive process, any deficit in the relational aspects of numbers used in time or measurement attributes such as fractions, are very likely to cause misconceptions in the understanding of physical time – that is measurement by clock and calendar.  Therefore concrete models allow the language of time to be directly associated with the concept at hand. For example, in an investigation by McMillen & Ortiz-Hernandez (2008), students explored fractions of time with materials of both a discrete (connecting cubes to represent minutes) and continuous nature (number lines representing a calendar) to explore quarter and half – the language used to describe a duration of time.  This study found that students who worked with such models built a robust ‘understanding of concepts of time and the ways it is measured, rather than learning just to tell time’ (McMillen et.al 2008, p. 255). To get a sense of how complex the concept of time is, consider the following schema which illustrates the connectedness of the skills and concepts required under the "umbrella" of time:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

McMillen et.al (2008), Hiebert (2013); and Star (2013) all concur, that traditional methods of learning to read and tell the time in primary school classes has been one of rote learning – disguised as the integration between several skills or procedures (not concepts) such as group counting by rote and shape recognition (in relation to 'portions' of a clock face). In contrast to focusing on rote learning procedures, McMillen et.al (2008) argue the duration of time and relating this to the symbols (numbers) on a clock face are essential to a deep conceptual understanding of time, yet typically not the focus of lessons on time in middle primary schooling. These issues illustrated in the above literature became the inspiration for this teaching and learning resource.